In Bayesian statistics, posterior probability distribution is typically used to update our prior beliefs after accounting for the likelihood of observing certain data. In complicated models, it may not be feasible to work out the posterior distribution, especially with unknown parameters. Thus, simulation methods are used to approximate the posterior instead. This blog post presents the application of a simulation method termed grid approximation to estimate the win rate of top football teams in the current English Premier League 24/25 season.

Grid Approximation
Bayesian statistics provide a framework of updating our beliefs based on evidence observed. At the core of this framework is Bayes’ Theorem, which relies on three key components: the prior probability, the likelihood and the posterior probability.The posterior probability represents an updated belief about a parameter or hypothesis after considering the prior knowledge and the observed data. It can be expressed as a conditional probability derived from the prior and the likelihood. When working with continuous variables, the posterior probability is typically represented as a distribution, calculated as the product of the prior distribution and the likelihood, normalised to ensure it forms a valid probability distribution.
Grid approximation is one approach to estimate a posterior probability distribution. It involves creating a grid of possible parameter values and calculating the posterior probability for each value. By evaluating the posterior across the grid, this approach provides an approximation of the entire posterior distribution in a simple and systematic way.
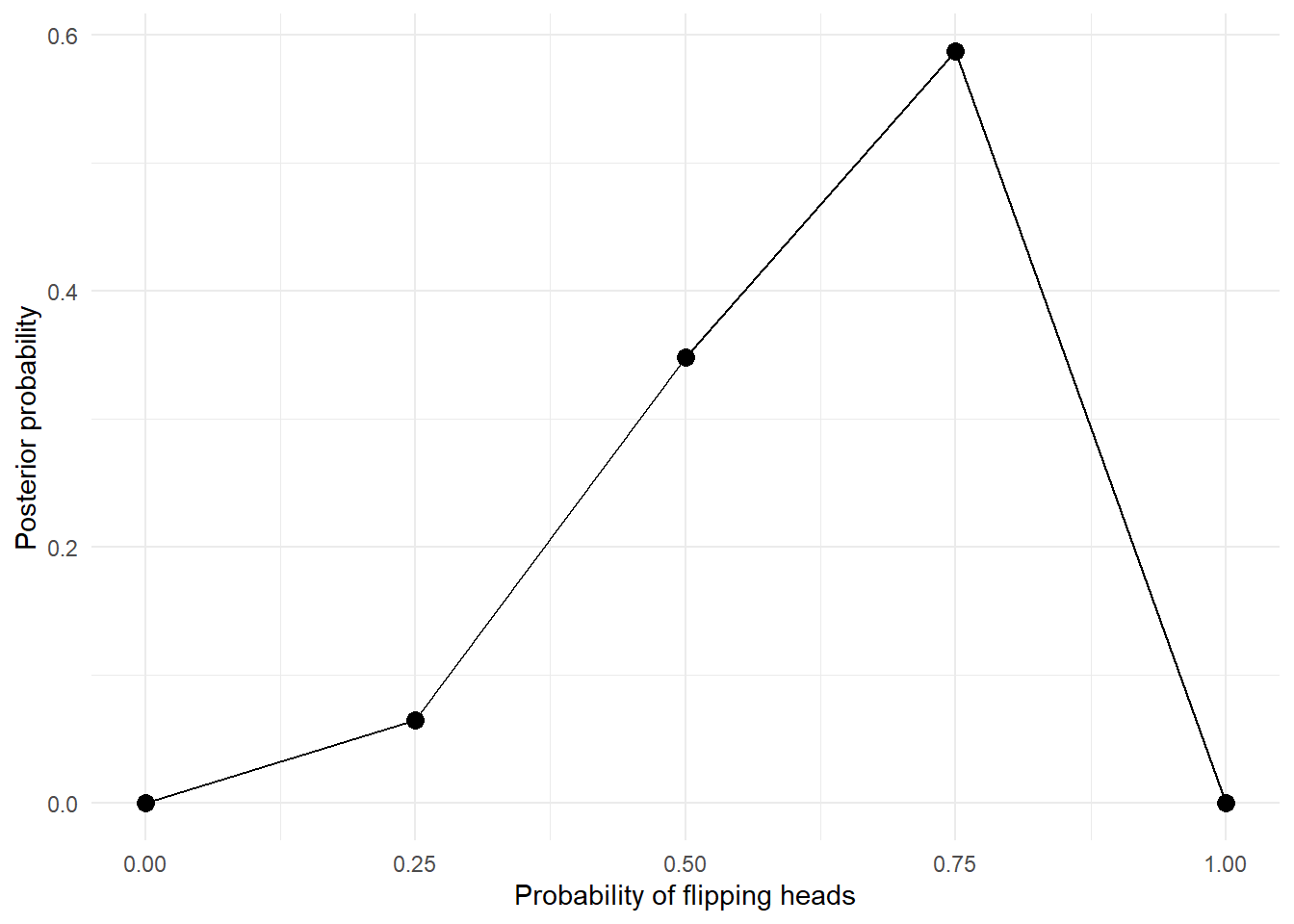
For example, let’s assume that we have a biased coin and we like to estimate its probability of flipping heads. We performed some coin flips and observed that there were three heads out of four flips. We may estimate the posterior probability distribution by computing the likelihood of observing the data using some selected values (e.g., 0, 0.25, 0.5, 0.75, 1). These values are referred as the grid in this estimation method. The visualisation below plots the computed posterior probability at each of the five values. In doing so, we can see an approximation of the posterior probability distribution.
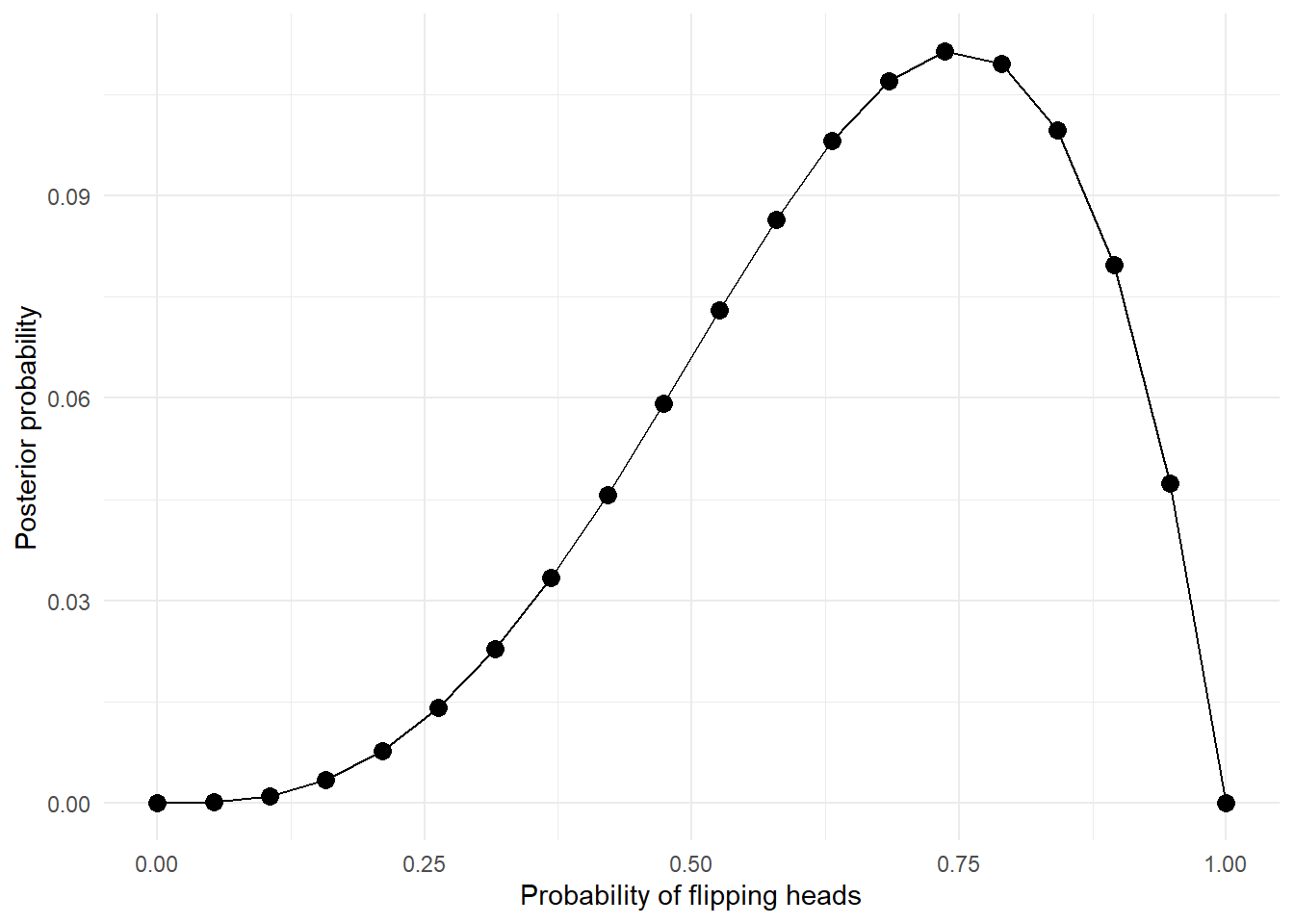
The appeal of this estimation method lies in its simplicity. By increasing the grid density with more points, the precision of the estimation improves. The visualisation below demonstrates an example using twenty grid points, resulting in a noticeably smoother curve for the posterior probability distribution.
Grid approximation works extremely well in simple models with few parameters. In this blog post, I applied this simulation method to estimate the win rate of top football teams in the English Premier League given the results that we have observed so far in the current 24/25 season.
At the point of writing, most teams have played seventeen games with Liverpool leading the table. The table below shows the current descriptive statistics of selected top teams in the league.
Steps for Grid Approximation Modelling
Taking reference from Richard McElreath’s awesome Statistical Rethinking book, building a grid approximation model involves five steps.
Define the grid by deciding how many points to use in estimating the posterior probability distribution.
Define your prior probability distribution.
Compute the likelihood of observing the data at each value in the defined grid.
Compute the unstandardised posterior at each grid parameter value by multiplying the prior by the likelihood.
Standardise the posterior probability to a value between 0 and 1.
Importance of Priors
At the core of Bayesian statistics is the process of updating our initial beliefs based on new evidence. These initial beliefs, known as priors, play a crucial role in shaping the analysis. Priors encapsulate our assumptions and knowledge about the parameters or model before any data is observed, providing a starting point for inference. The choice of prior can significantly influence the results, especially when data is limited or uncertain, making it essential to select priors thoughtfully to ensure they reflect the context and goals of the analysis. In this blog post, we will examine the difference between an ignorant and informative prior to make inference about a team’s win rate.
A Naive Spectator
Imagine you are entirely new to football and know nothing about the teams or their historical performances. You are unable to tell which teams are stronger or weaker. The only information you have to infer a team’s win rate is their performance so far this season. This absence of prior knowledge is called a flat prior, where equal probability is assigned to all possible win rates from 0% to 100%.
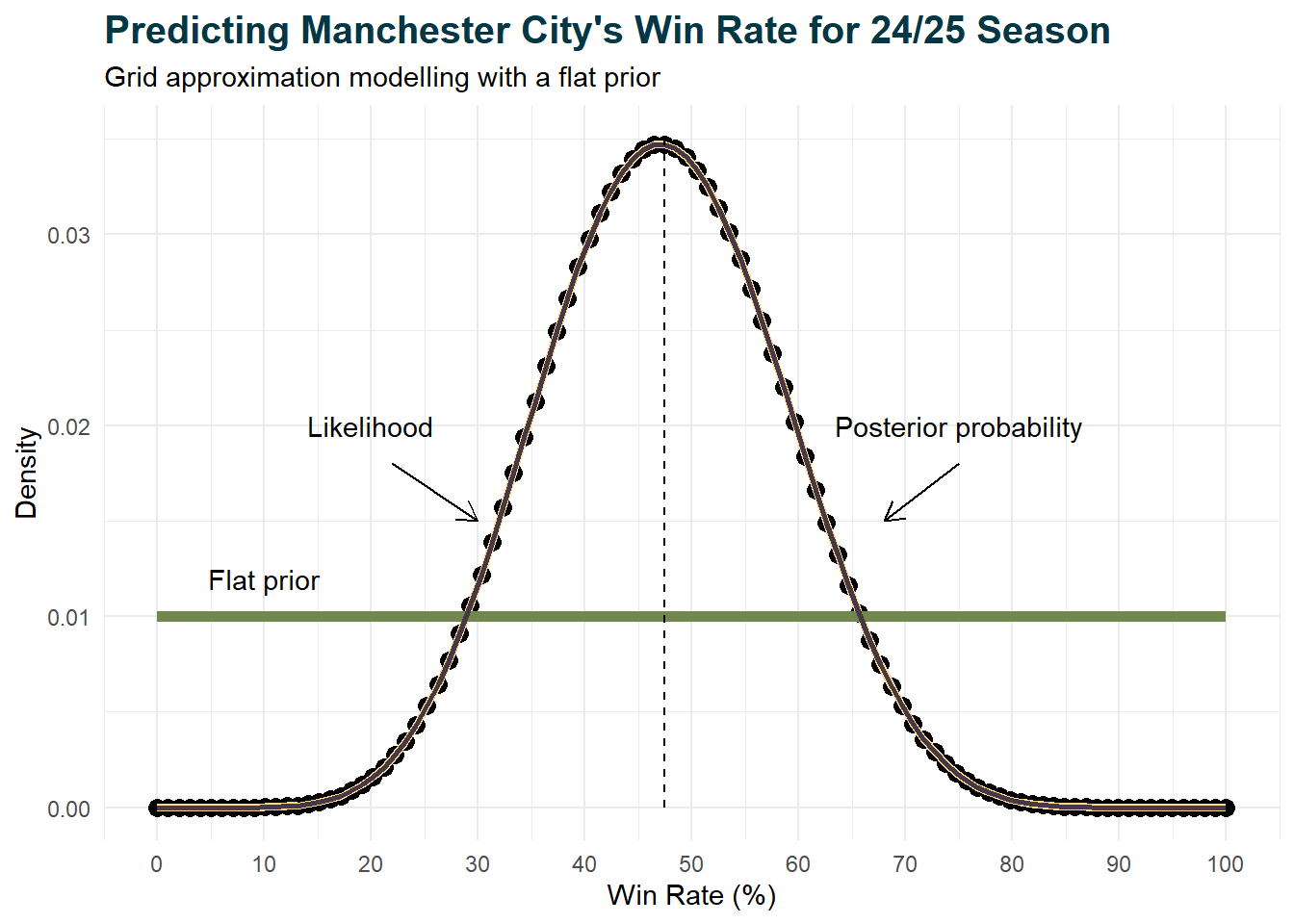
The code below shows how we can build our grid approximation model to predict a team’s win rate using the five steps listed above. In this example, we built a model to predict the win rate of reigning champions, Manchester City, given their performance so far in the current season. First, we define a grid using 100 points that range between 0 and 1, representing the possible win rates. Second, we use a flat prior to reflect our naive beliefs by choosing a uniform distribution that assigns the same probability to every possible win-rate. Third, we compute the likelihood of observing eight wins out of 17 games based on each value in the defined grid. Fourth, we compute the unstandardised posterior probability by simply multiplying the likelihood and prior together. Last, we standardise the posterior probability to a value between 0 and 1.
# Step 1: Define grid
p_grid <- seq(from=0, to=1, length.out=100)
# Step 2: Define prior
prior <- rep( 1 , length(p_grid))
# Step 3: Compute likelihood at each value in grid
# Likelihood of observing Man City's 8 wins out of 17 games
likelihood <- dbinom(8 , size=17 , prob=p_grid)
# Step 4: Compute product of likelihood and prior
unstd.posterior <- likelihood * prior
# Step 5: Standardise the posterior
posterior <- unstd.posterior / sum(unstd.posterior)The visualisation below shows the three key components of our model. Notably, the likelihood and posterior probability distributions are superimposed on one another due to the flat prior used. In absence of any prior information, the posterior probability is primarily computed from the data observed. The dashed line represents the parameter value with the highest posterior probability, also termed the maximum a posteriori (MAP) estimate. In this case, the MAP was estimated to be 47.5%, which corresponds closely to the probability derived from the data observed.
A Wise Fan
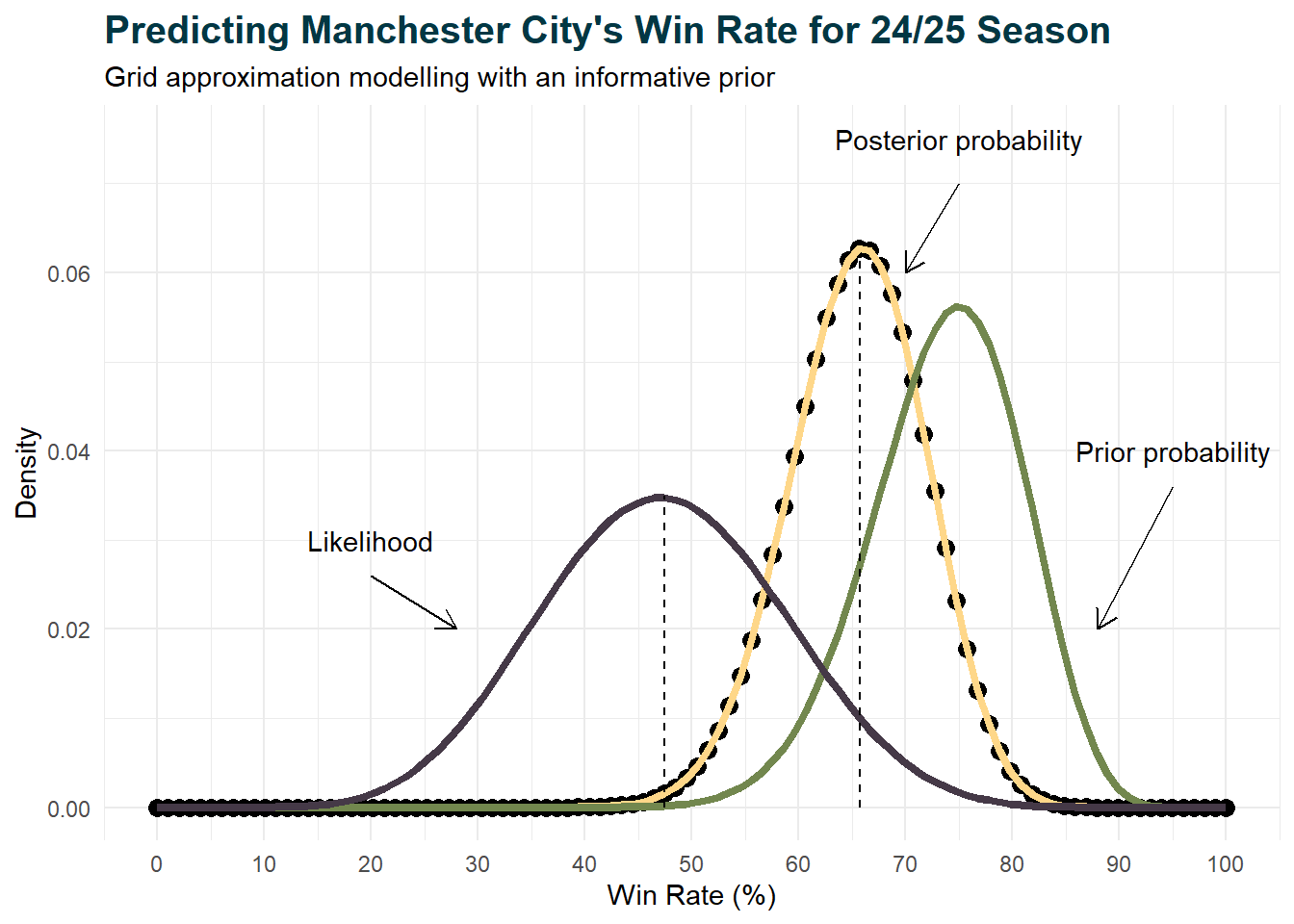
Based on the observed data alone, a naive observer might not recognise Manchester City as an exceptionally strong team. However, for anyone familiar with the league, this inference would seem far from accurate. Considering that Manchester City has won six league titles in the past seven seasons, it would be absurd to dismiss their prowess. In contrast, seasoned football fans would reasonably anticipate the team to rebound with a higher win rate, given their consistent track record of success Next, let’s model the posterior probability distribution with a more informative prior.
The table below shows the total number of wins achieved by each team over the past three seasons. Manchester City has averaged 28 wins per season out of 38 games, corresponding to an impressive win rate of 73.7%. A well-informed fan armed with this knowledge is likely to hold significantly different prior beliefs.
The only thing that we have to change is the prior specification. In this case, we define our prior using a beta distribution since it models continuous random variables between 0 and 1, which aligns with how a win rate distribution should look like. We use the average proportion of wins to define the shape of the beta distribution, with α = 28 and β = 10.
# Step 1: Define grid
p_grid <- seq(from=0, to=1, length.out=100)
# Step 2: Define prior
# Informative prior using a beta distribution
prior <- dbeta(p_grid, 28, 10)
# Step 3: Compute likelihood at each value in grid
# Likelihood of observing Man City's 8 wins out of 17 games
likelihood <- dbinom(8 , size=17 , prob=p_grid)
# Step 4: Compute product of likelihood and prior
unstd.posterior <- likelihood * prior
# Step 5: Standardise the posterior
posterior <- unstd.posterior / sum(unstd.posterior)The figure below visualises the grid approximation model. Unlike the flat prior model, the likelihood and posterior probability distributions exhibit notable differences. With an informative prior, the MAP was estimated to be at 65.7% instead, which lies between the peaks of the likelihood and prior probability distributions.
Prediction of Win Rates
Different priors could lead to different conclusions on the same data observed. The table below presents the predicted win rates of respective teams based on the flat prior and informative prior models, with simple inference made using the MAP parameter.
The comparison of models provides useful insights on the different prediction estimates. The differences highlight the importance of our prior selection. If you are a football fan, the informative prior model is likely more aligned with your beliefs. As posited by the wisdom of the crowd concept, considering different estimates from different models can probably lead to more accurate and robust predictions.
Round-Up
This blog post explored the use of grid approximation to model the win rates of top football teams in the English Premier League. I demonstrated how different priors can lead to different inferences based the same observed data. British statistician George Box famously said ‘All models are wrong, but some are useful’. This is probably too simplistic a model to predict win rates of football team as we did not account for possibly important variables. Nevertheless, this simple model can still be useful to better inform our guesses. The heart of Bayesian statistics is the continuous update of our beliefs, and we can better refine our model with new data observed over the season.
How accurate will these predictions be? Check back in May to find out!